double pendulum using lagrangian mechanics
The double pendulum is the classic example of a chaotic system. But using lagrangian mechanics we can solve this problem analytically. Here we will analyse a double pendulum that can be moved horizontally by it's support. We will try to get a formula for the angle acceleration dependent on the acceleration of the support. Once we have the acceleration, speed and position are easy. First we do a single pendulum to practice ;)
single pendulum
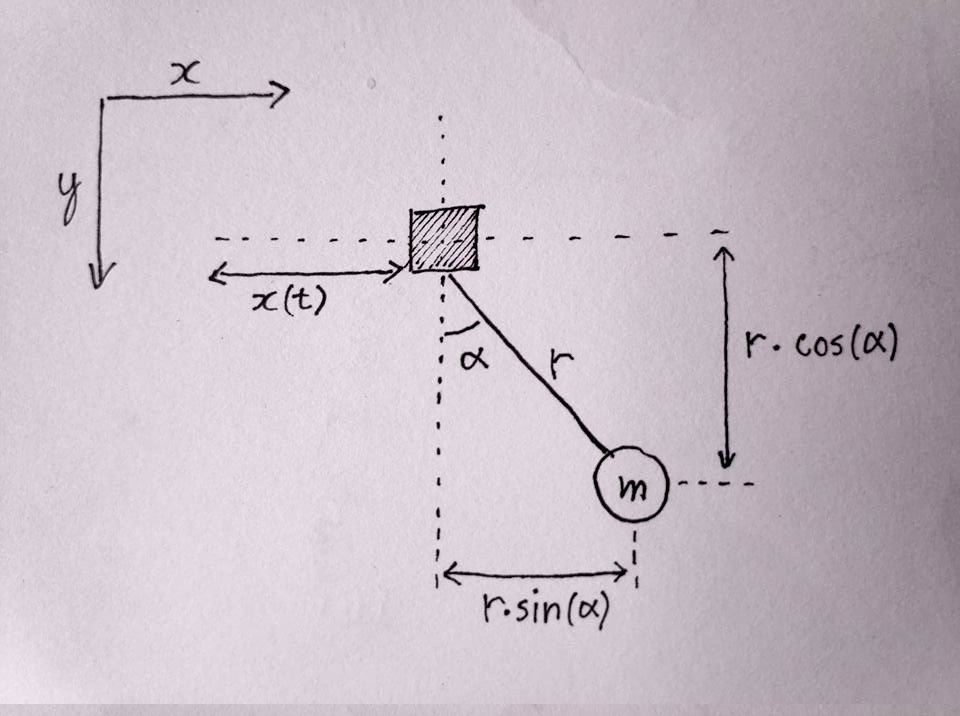
At the end we want an equation for \(\ddot{\alpha}\) dependent on \(x\), \(\alpha\) or their derivatives. From \(\ddot{\alpha}\) its easy to get \(\dot{\alpha}\) and \(\alpha\). These we can then use to render the pendulum on screen.
The langrangian is defined as L = T - V, where T is the kinetic energy and V is the potential energy. To calculate the kinetic energy we need the velocity \(v\) of the ball, which we can calculate from it's components \(v_x\) and \(v_y\):
$$ \begin{align} v_x &= \dot{x} + \dot{\alpha} r \cos(\alpha) \\ v_y &= \dot{\alpha} r \sin(\alpha) \\ \implies v^2 &= v_x^2 + v_y^2 \\ &= \left( \dot{x} + \dot{\alpha} r \cos(\alpha) \right)^2 + \left( \dot{\alpha} r \sin(\alpha) \right)^2 \\ &= \dot{x}^2 + 2 \dot{\alpha} \dot{x} r \cos(\alpha) + \dot{\alpha}^2 r^2 \end{align} $$
Then kinetic energy is
$$ \begin{align} T &= \frac{1}{2} m v^2 \\ &= \frac{1}{2} m \left[ \dot{x}^2 + 2 \dot{\alpha} \dot{x} r \cos(\alpha) + \dot{\alpha}^2 r^2 \right] \end{align} $$
and potential energy is
$$ \begin{align} V &= m g h \\ &= -m g r \cos(\alpha) \end{align} $$
so the lagrangian is then
$$ \begin{align} L &= T - V \\ &= \frac{1}{2} m \left[ \dot{x}^2 + 2 \dot{\alpha} \dot{x} r \cos(\alpha) + \dot{\alpha}^2 r^2 \right] + m g r \cos(\alpha) \end{align} $$
then to get a useful equation for \( \ddot{\alpha} \) we have to solve
$$ \frac{d}{dt} \frac{\partial L}{\partial \dot{\alpha}} - \frac{\partial L}{\partial \alpha} = Q_j = \frac{\partial P}{\partial \dot{\alpha}} $$
where \( Q_j \) are the dissipative forces i.e. the friction force in this case.
$$ F_{friction} = -\mu v $$
so the dissipation function is
$$ P = - \frac{1}{2} \mu v^2 = - \frac{1}{2} \mu \left[ \dot{x}^2 + 2 \dot{\alpha} \dot{x} r \cos(\alpha) + \dot{\alpha}^2 r^2 \right] $$
The partial derivatives are:
$$ \begin{align} \frac{\partial L}{\partial \dot{\alpha}} &= m r^2 \dot{\alpha} + m \dot{x} r \cos(\alpha) \\ \frac{\partial L}{\partial \alpha} &= -m \dot{x} r \dot{\alpha} \sin(\alpha) - m g r \sin(\alpha) \\ \frac{\partial P}{\partial \dot{\alpha}} &= - \mu r^2 \dot{\alpha} - \mu \dot{x} r \cos(\alpha) \end{align} $$
so we need to solve
$$ \begin{align} \frac{d}{dt} \left( m r^2 \dot{\alpha} + m \dot{x} r \cos(\alpha) \right) + m \dot{x} r \dot{\alpha} \sin(\alpha) + m g r \sin(\alpha) & = - \mu r^2 \dot{\alpha} - \mu \dot{x} r \cos(\alpha) \\ r^2 \ddot{\alpha} + \ddot{x} r \cos(\alpha) - \dot{x} r \dot{\alpha} \sin(\alpha) + \dot{x} r \dot{\alpha} \sin(\alpha) + g r \sin(\alpha) &= - \frac{\mu}{m} r^2 \dot{\alpha} - \frac{\mu}{m} \dot{x} r \cos(\alpha) \\ r^2 \ddot{\alpha} &= - \frac{\mu}{m} r^2 \dot{\alpha} - \frac{\mu}{m} \dot{x} r \cos(\alpha) - \ddot{x} r \cos(\alpha) - g r \sin(\alpha) \\ \ddot{\alpha} &= - \frac{\mu}{m} \dot{\alpha} - \frac{\mu}{mr} \dot{x} \cos(\alpha) - \frac{\ddot{x}}{r} \cos(\alpha) - \frac{g}{r} \sin(\alpha) \\ \end{align} $$
Now we have all the formula's to show a simple pendulum (the angle itself is just \(\alpha = \ddot{\alpha} \cdot t^2\)):
double pendulum
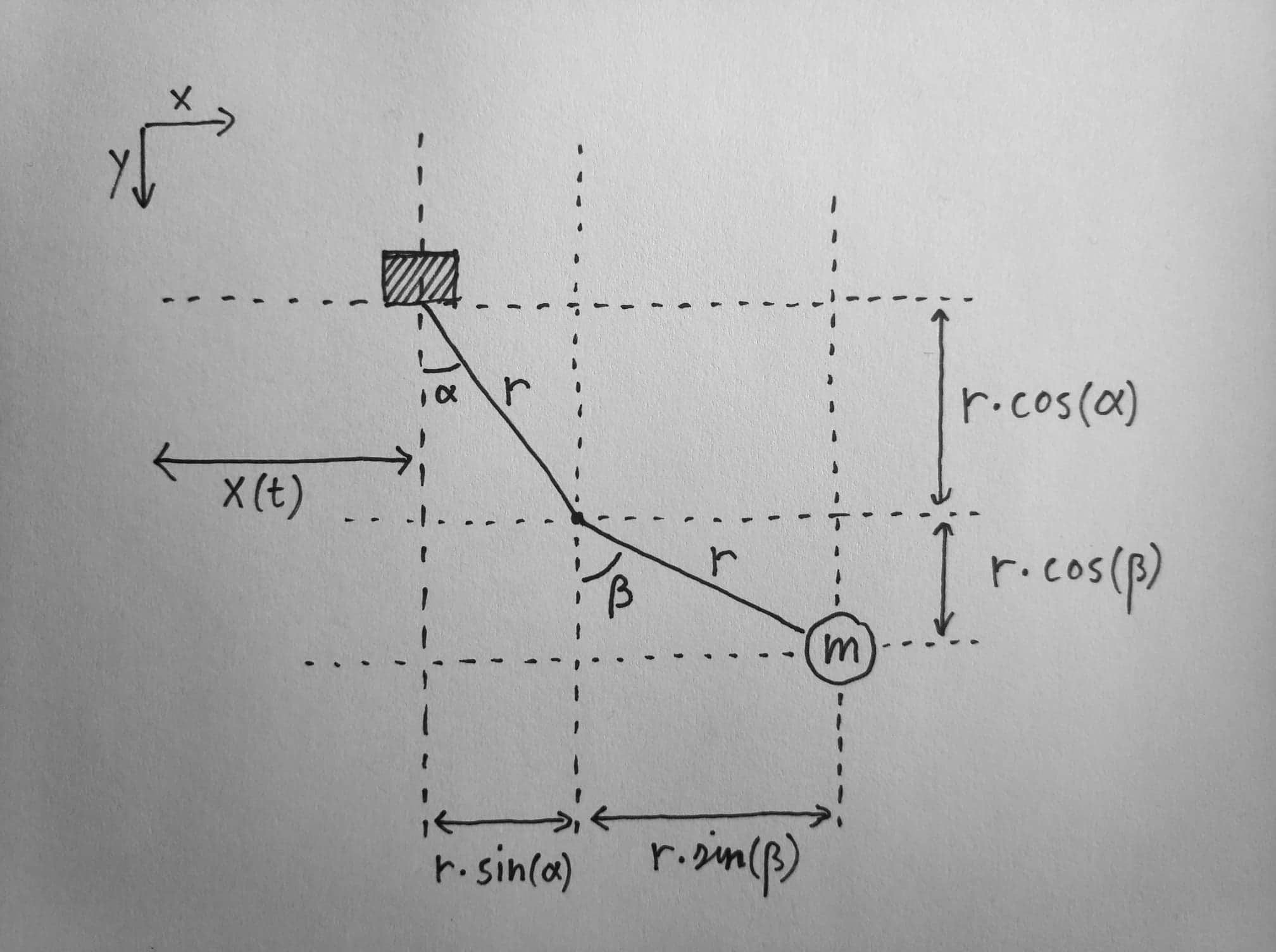
Now we do the exact same thing for the double pendulum.
The velocity \(v_1\) of the first ball is the same as in the single pendulum, i.e.:
$$ v_1^2 = \dot{x}^2 + 2 \dot{\alpha} \dot{x} r \cos(\alpha) + \dot{\alpha}^2 r^2 $$
the velocity of the second ball is:
$$ \begin{align} v_x &= \dot{x} + \dot{\alpha} r \cos(\alpha) + \dot{\beta} r \cos(\beta) \\ v_y &= \dot{\alpha} r \sin(\alpha) + \dot{\beta} r \sin(\beta) \\ \implies v_2^2 &= v_x^2 + v_y^2 \\ &= \left( \dot{x} + \dot{\alpha} r \cos(\alpha) + \dot{\beta} r \cos(\beta) \right)^2 + \left( \dot{\alpha} r \sin(\alpha) + \dot{\beta} r \sin(\beta) \right)^2 \\ &= \dot{x}^2 + 2 \dot{x} \dot{\alpha} r \cos(\alpha) + 2 \dot{x} \dot{\beta} r \cos(\beta) + \dot{\alpha}^2 r^2 \cos^2(\alpha) + 2 \dot{\alpha} r \cos(\alpha) \dot{\beta} r \cos(\beta) + \dot{\beta}^2 r^2 \cos^2(\beta) + \dot{\alpha}^2 r^2 \sin^2(\alpha) + 2 \dot{\alpha} r \sin(\alpha) \dot{\beta} r \sin(\beta) + \dot{\beta}^2 r^2 \sin^2(\beta) \\ &= \dot{x}^2 + 2 \dot{x} \dot{\alpha} r \cos(\alpha) + 2 \dot{x} \dot{\beta} r \cos(\beta) + \dot{\alpha}^2 r^2 + \dot{\beta}^2 r^2 + 2 r^2 \dot{\alpha} \dot{\beta} \left( \cos(\alpha) \cos(\beta) + \sin(\alpha) \sin(\beta) \right) \\ &= \dot{x}^2 + 2 \dot{x} \dot{\alpha} r \cos(\alpha) + 2 \dot{x} \dot{\beta} r \cos(\beta) + \dot{\alpha}^2 r^2 + \dot{\beta}^2 r^2 + 2 r^2 \dot{\alpha} \dot{\beta} \cos(\alpha - \beta) \end{align} $$
Then kinetic energy is
$$ \begin{align} T &= \frac{1}{2} m \left[ v_1^2 + v_2^2 \right] \\ &= \frac{1}{2} m \left[ \dot{x}^2 + 2 \dot{\alpha} \dot{x} r \cos(\alpha) + \dot{\alpha}^2 r^2 + \dot{x}^2 + 2 \dot{x} \dot{\alpha} r \cos(\alpha) + 2 \dot{x} \dot{\beta} r \cos(\beta) + \dot{\alpha}^2 r^2 + \dot{\beta}^2 r^2 + 2 r^2 \dot{\alpha} \dot{\beta} \cos(\alpha - \beta) \right] \\ &= \frac{1}{2} m \left[ 2 \dot{x}^2 + 4 \dot{\alpha} \dot{x} r \cos(\alpha) + 2 \dot{\alpha}^2 r^2 + 2 \dot{x} \dot{\beta} r \cos(\beta) + \dot{\beta}^2 r^2 + 2 r^2 \dot{\alpha} \dot{\beta} \cos(\alpha - \beta) \right] \end{align} $$
and potential energy is
$$ \begin{align} V &= m g \left[ h_1 + h_2 \right] \\ &= -m g r \left[ 2 \cos(\alpha) + \cos(\beta) \right] \end{align} $$
so the lagrangian is then
$$ \begin{align} L &= T - V \\ &= \frac{1}{2} m \left[ 2 \dot{x}^2 + 4 \dot{\alpha} \dot{x} r \cos(\alpha) + 2 \dot{\alpha}^2 r^2 + 2 \dot{x} \dot{\beta} r \cos(\beta) + \dot{\beta}^2 r^2 + 2 r^2 \dot{\alpha} \dot{\beta} \cos(\alpha - \beta) \right] + m g r \left[ 2 \cos(\alpha) + \cos(\beta) \right] \end{align} $$
then to get a useful equation for \( \ddot{\alpha} \) and \( \ddot{\beta} \) have to solve
$$ \frac{d}{dt} \frac{\partial L}{\partial \dot{\alpha}} - \frac{\partial L}{\partial \alpha} = 0 \quad \text{and} \quad \frac{d}{dt} \frac{\partial L}{\partial \dot{\beta}} - \frac{\partial L}{\partial \beta} = 0 $$
We will ignore friction this time and add an approximation later (I actually tried to do it with friction just like with the single pendulum, but I couldn't make it work!). Now lets start with the \( \alpha \) case. The partial derivatives are:
$$ \begin{align} \frac{\partial L}{\partial \dot{\alpha}} &= 2 m \dot{x} r \cos(\alpha) + 2 m r^2 \dot{\alpha} + m r^2 \dot{\beta} \cos(\alpha - \beta) \\ \frac{\partial L}{\partial \alpha} &= - 2 m \dot{x} r \dot{\alpha} \sin(\alpha) - m r^2 \dot{\alpha} \dot{\beta} \sin(\alpha - \beta) - 2 m g r \sin(\alpha) \end{align} $$
so we need to solve
$$ \begin{align} 0 &= \frac{d}{dt} \left( 2 m \dot{x} r \cos(\alpha) + 2 m r^2 \dot{\alpha} + m r^2 \dot{\beta} \cos(\alpha - \beta) \right) + 2 m \dot{x} r \dot{\alpha} \sin(\alpha) + m r^2 \dot{\alpha} \dot{\beta} \sin(\alpha - \beta) + 2 m g r \sin(\alpha) \\ 0 &= 2 r^2 \ddot{\alpha} + 2 \ddot{x} r \cos(\alpha) - 2 \dot{x} r \dot{\alpha} \sin(\alpha) + r^2 \left( \ddot{\beta} \cos(\alpha - \beta) - \dot{\beta} \sin(\alpha - \beta) \left( \dot{\alpha} - \dot{\beta} \right) \right) + 2 \dot{x} r \dot{\alpha} \sin(\alpha) + r^2 \dot{\alpha} \dot{\beta} \sin(\alpha - \beta) + 2 g r \sin(\alpha) \\ 0 &= 2 r^2 \ddot{\alpha} + 2 \ddot{x} r \cos(\alpha) + r^2 \left( \ddot{\beta} \cos(\alpha - \beta) - \dot{\beta} \sin(\alpha - \beta) \left( \dot{\alpha} - \dot{\beta} \right) \right) + r^2 \dot{\alpha} \dot{\beta} \sin(\alpha - \beta) + 2 g r \sin(\alpha) \\ 0 &= \ddot{\alpha} + \frac{\ddot{x}}{r} \cos(\alpha) + \frac{1}{2} \ddot{\beta} \cos(\alpha - \beta) - \frac{1}{2} \dot{\beta} \sin(\alpha - \beta) \left( \dot{\alpha} - \dot{\beta} \right) + \frac{1}{2} \dot{\alpha} \dot{\beta} \sin(\alpha - \beta) + \frac{g}{r} \sin(\alpha) \\ \ddot{\alpha} &= - \frac{1}{2} \dot{\alpha} \dot{\beta} \sin(\alpha - \beta) - \frac{g}{r} \sin(\alpha) - \frac{\ddot{x}}{r} \cos(\alpha) - \frac{1}{2} \ddot{\beta} \cos(\alpha - \beta) + \frac{1}{2} \dot{\beta} \sin(\alpha - \beta) \left( \dot{\alpha} - \dot{\beta} \right) \end{align} $$
Now the \( \beta \) case. The partial derivatives are:
$$ \begin{align} \frac{\partial L}{\partial \dot{\beta}} &= m \dot{x} r \cos(\beta) + m r^2 \dot{\beta} + m r^2 \dot{\alpha} \cos(\alpha - \beta) \\ \frac{\partial L}{\partial \beta} &= - m \dot{x} r \dot{\beta} \sin(\beta) + m r^2 \dot{\alpha} \dot{\beta} \sin(\alpha - \beta) - m g r \sin(\beta) \end{align} $$
so we need to solve
$$ \begin{align} 0 &= \frac{d}{dt} \left( m \dot{x} r \cos(\beta) + m r^2 \dot{\beta} + m r^2 \dot{\alpha} \cos(\alpha - \beta) \right) + m \dot{x} r \dot{\beta} \sin(\beta) - m r^2 \dot{\alpha} \dot{\beta} \sin(\alpha - \beta) + m g r \sin(\beta) \\ 0 &= r^2 \ddot{\beta} + \ddot{x} r \cos(\beta) - \dot{x} r \dot{\beta} \sin(\beta) + r^2 \left( \ddot{\alpha} \cos(\alpha - \beta) - \dot{\alpha} \sin(\alpha - \beta) \left( \dot{\alpha} - \dot{\beta} \right) \right) + \dot{x} r \dot{\beta} \sin(\beta) - r^2 \dot{\alpha} \dot{\beta} \sin(\alpha - \beta) + g r \sin(\beta) \\ 0 &= r^2 \ddot{\beta} + \ddot{x} r \cos(\beta) + r^2 \left( \ddot{\alpha} \cos(\alpha - \beta) - \dot{\alpha} \sin(\alpha - \beta) \left( \dot{\alpha} - \dot{\beta} \right) \right) - r^2 \dot{\alpha} \dot{\beta} \sin(\alpha - \beta) + g r \sin(\beta) \\ 0 &= \ddot{\beta} + \frac{\ddot{x}}{r} \cos(\beta) + \ddot{\alpha} \cos(\alpha - \beta) - \dot{\alpha} \sin(\alpha - \beta) \left( \dot{\alpha} - \dot{\beta} \right) - \dot{\alpha} \dot{\beta} \sin(\alpha - \beta) + \frac{g}{r} \sin(\beta) \\ \ddot{\beta} &= \dot{\alpha} \dot{\beta} \sin(\alpha - \beta) - \frac{g}{r} \sin(\beta) - \frac{\ddot{x}}{r} \cos(\beta) - \ddot{\alpha} \cos(\alpha - \beta) + \dot{\alpha} \sin(\alpha - \beta) \left( \dot{\alpha} - \dot{\beta} \right) \end{align} $$
now we just add a friction term to both formulas proportional to the angular velocity, to get to our final formulas:
$$ \begin{align} \ddot{\alpha} &= - \frac{1}{2} \dot{\alpha} \dot{\beta} \sin(\alpha - \beta) - \frac{g}{r} \sin(\alpha) - \frac{\ddot{x}}{r} \cos(\alpha) - \frac{1}{2} \ddot{\beta} \cos(\alpha - \beta) + \frac{1}{2} \dot{\beta} \sin(\alpha - \beta) \left( \dot{\alpha} - \dot{\beta} \right) - \mu \dot{\alpha} \\ \ddot{\beta} &= \dot{\alpha} \dot{\beta} \sin(\alpha - \beta) - \frac{g}{r} \sin(\beta) - \frac{\ddot{x}}{r} \cos(\beta) - \ddot{\alpha} \cos(\alpha - \beta) + \dot{\alpha} \sin(\alpha - \beta) \left( \dot{\alpha} - \dot{\beta} \right) - \mu \dot{\beta} \end{align} $$
Here is the simulated result:
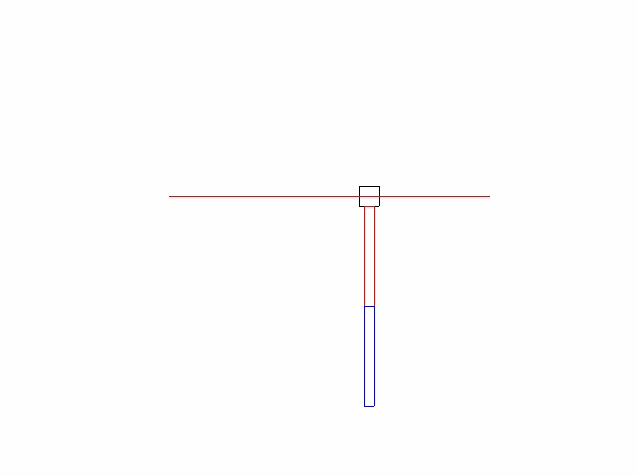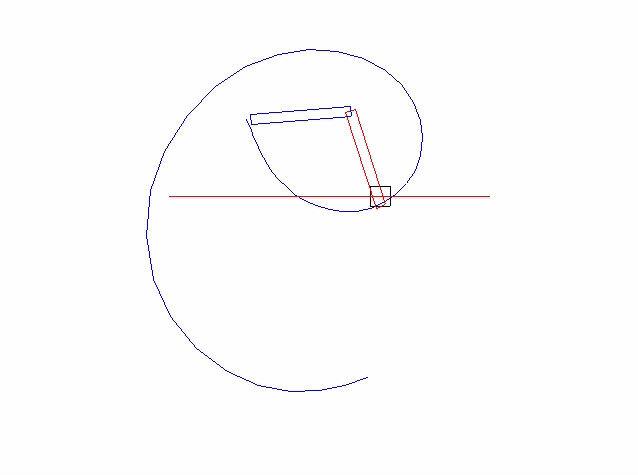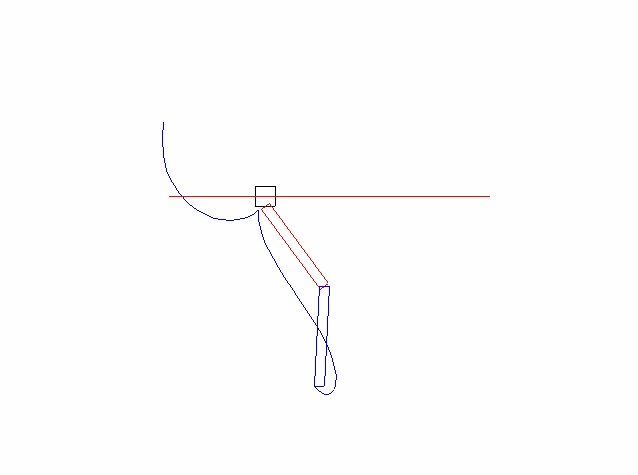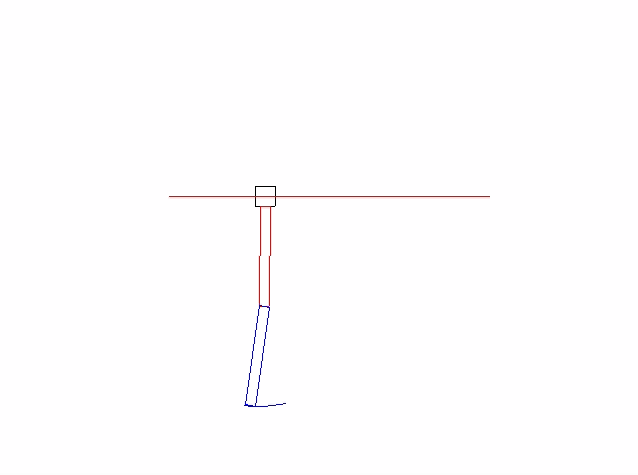
C code
Here is my implementation in C with SDL. This code was used to create the last gif. The lines where the two derived formulas get used are highlighted.
:::c hl_lines="259 260 261 262 263 264 273 274 275 276 277 278"
#include <stdio.h>
#include <stdbool.h>
#include "stdint.h"
#include <SDL2/SDL.h>
#include <math.h>
#define PI 3.14159265
#define SCREEN_WIDTH 640
#define SCREEN_HEIGHT 480
#define PATH_L 50
SDL_Window* gWindow = NULL;
SDL_Renderer* gRenderer = NULL;
const uint8_t* gKeyboard;
typedef struct {
float x, y;
} v2;
static inline v2 V2(float x, float y) {
return (v2){x, y};
}
static inline int floatToInt(float x) {
return (int)(x + 0.5);
}
static inline SDL_Point v2ToSDLpt(v2 a) {
return (SDL_Point){floatToInt(a.x), floatToInt(a.y)};
}
static inline void v2sToPts(v2 v2s[], SDL_Point pts[], int count) {
for (int i = 0; i < count; i++) {
pts[i] = v2ToSDLpt(v2s[i]);
}
}
static inline v2 v2_add(v2 a, v2 b) {
return (v2){a.x + b.x, a.y + b.y};
}
static inline void v2s_add_v2(v2* v2s, int count, v2 b) {
for (int i = 0; i < count; i++) {
v2s[i] = (v2){v2s[i].x + b.x, v2s[i].y + b.y};
}
}
static inline v2 v2_sub(v2 a, v2 b) {
return (v2){a.x - b.x, a.y - b.y};
}
static inline v2 v2_scale(v2 a, float b) {
return (v2){a.x * b, a.y * b};
}
static inline void v2_print(v2 a) {
printf("x = %f, y = %f\n", a.x, a.y);
}
static inline void v2s_rot(v2* pts, int count, v2 origin, float angle) {
// move to origin
for (int i = 0; i < count; i++) {
pts[i] = v2_sub(pts[i], origin);
}
// rotate points counter clock wise
v2 p;
float cosangle = cosf(-angle);
float sinangle = sinf(-angle);
for (int i = 0; i < count; i++) {
p = pts[i];
pts[i] = (v2){cosangle*p.x - sinangle*p.y,
sinangle*p.x + cosangle*p.y};
}
// move back
for (int i = 0; i < count; i++) {
pts[i] = v2_add(pts[i], origin);
}
}
bool initSDL() {
// initialize SDL
if (SDL_Init(SDL_INIT_VIDEO) < 0) {
printf("SDL could not initialize! SDL_Error: %s\n",
SDL_GetError());
return false;
}
// create window
gWindow = SDL_CreateWindow("pendulum",
SDL_WINDOWPOS_UNDEFINED,
SDL_WINDOWPOS_UNDEFINED,
SCREEN_WIDTH,
SCREEN_HEIGHT,
SDL_WINDOW_SHOWN);
if (gWindow == NULL) {
printf("Window could not be created! SDL_Error: %s\n",
SDL_GetError());
return false;
}
// create renderer
gRenderer = SDL_CreateRenderer(gWindow, -1, SDL_RENDERER_PRESENTVSYNC);
if(gRenderer == NULL)
{
printf( "Renderer could not be created! SDL Error: %s\n", SDL_GetError() );
return false;
}
// initialize renderer color
SDL_SetRenderDrawColor(gRenderer, 255, 255, 255, 255);
// allow colors with alpha transparancy values
SDL_SetRenderDrawBlendMode(gRenderer, SDL_BLENDMODE_BLEND);
return true;
}
void closeSDL() {
// destroy window
if (gRenderer) {
SDL_DestroyRenderer(gRenderer);
gRenderer = NULL;
}
// destroy window
if (gWindow) {
SDL_DestroyWindow(gWindow);
gWindow = NULL;
}
// quit SDL subsystems
SDL_Quit();
}
static inline void drawRect(SDL_Renderer* renderer, v2 pos, v2 size,
v2 origin, float rotAngle) {
v2 vertices[5];
vertices[0] = pos;
vertices[1] = (v2){pos.x + size.x, pos.y};
vertices[2] = (v2){pos.x + size.x, pos.y + size.y};
vertices[3] = (v2){pos.x, pos.y + size.y};
vertices[4] = pos;
origin = v2_add(pos, V2(origin.x, origin.y));
v2s_rot(vertices, 5, origin, rotAngle);
SDL_Point pts[5];
v2sToPts(vertices, pts, 5);
SDL_RenderDrawLines(gRenderer, pts, 5);
}
typedef struct {
v2 pos, vel, acc;
} box;
int main(int argc, char* args[]) {
if (!initSDL()) {
printf("Failed to initialize SDL\n");
return 0;
}
bool quit = false;
// event handler
SDL_Event e;
// keeps track of time between steps
Uint32 newTime = 0, oldTime = 0;
// pendulum, consist of two legs:
// leg 1 placed right under support
// leg 2 placed right under leg 1
// both legs have the same width and height
int pendulumLength = 100;
float pendulumWidth = 10;
float gravity = 0.002;
float pendulumFrictionMassCoeff = 0.002; // pendulum friction coefficient divided by mass
v2 pendulumOrigin = V2(pendulumWidth / 2, 0);
// support and its track
float supportTrackHeight = 200;
float supportSize = 20;
float supportTrackStart = SCREEN_WIDTH / 4 + 0.5 * supportSize;
float supportTrackEnd = SCREEN_WIDTH * 3 / 4 + 0.5 * supportSize;
box support = {
{SCREEN_WIDTH / 2, supportTrackHeight - 0.5f*supportSize}, // pos
{0,0}, // vel
{0,0} // acc
};
float supportDrag = 0.8;
float supportControlSpeed = 0.005;
v2 leg1pos = {support.pos.x + (supportSize - pendulumWidth)*0.5f,
support.pos.y + supportSize}; // attachment point to support
float a = 0.0*PI; // pendulum angle alpha (angle leg 1)
float aVel = 0; // pendulum angle alpha velocity
float aAcc = 0; // pendulum angle alpha acceleration
v2 leg2pos; // attachment point to first leg
float b = 0; // pendulum angle beta (angle leg 2)
float bVel = 0; // pendulum angle beta velocity
float bAcc = 0; // pendulum angle beta acceleration
v2 path[PATH_L] = {0}; // pendulum tip path array
SDL_Point path_pts[PATH_L];
while (!quit) {
// handle events on queue
while (SDL_PollEvent(&e) != 0) {
if (e.type == SDL_QUIT) {
quit = true;
}
// update keyboard
gKeyboard = SDL_GetKeyboardState(NULL);
}
// clear screen, make background white
SDL_SetRenderDrawColor(gRenderer, 255, 255, 255, 255);
SDL_RenderClear(gRenderer);
// calculate time step
newTime = SDL_GetTicks();
float dt = (newTime - oldTime);
oldTime = newTime;
// -- physics update --
{
// update support support position
support.acc.x = 0;
if (gKeyboard[SDL_SCANCODE_RIGHT] && support.pos.x < supportTrackEnd - 0.5*supportSize) {
support.acc.x = supportControlSpeed;
}
if (gKeyboard[SDL_SCANCODE_LEFT] && support.pos.x > supportTrackStart - 0.5*supportSize) {
support.acc.x = -supportControlSpeed;
}
support.vel.x = support.vel.x + support.acc.x * dt;
support.vel.x *= supportDrag;
support.pos.x = support.pos.x + support.vel.x * dt;
// update pendulum leg 1 origin position
leg1pos.x = leg1pos.x + support.vel.x * dt;
// update pendulum leg 1 rotation angle
//aAcc = (-g*sin(a) - support.acc.x*cos(a))/l; // single pendulum without friction
//aAcc = - (g*sin(a) + support.acc.x*cos(a))/l - pendulumFrictionMassCoeff*(aVel + 1/l*support.vel.x*cosf(a)); // single pendulum with friction
aAcc = - 1/2*aVel*bVel*sinf(a-b)
- gravity/pendulumLength*sinf(a)
- support.acc.x/pendulumLength*cosf(a)
- 1/2*bAcc*cosf(a-b)
+ 1/2*bVel*sinf(a-b)*(aVel-bVel)
- pendulumFrictionMassCoeff*aVel; // friction approximation
aVel += aAcc * dt;
a += aVel * dt;
// update pendulum leg 2 position
leg2pos = V2(leg1pos.x + pendulumLength*sinf(a),
leg1pos.y + pendulumLength*cosf(a));
// update pendulum leg 2 rotation angle
bAcc = + aVel*bVel*sinf(a-b)
- gravity/pendulumLength*sinf(b)
- support.acc.x/pendulumLength*cosf(b)
- aAcc*cosf(a-b)
+ aVel*sinf(a-b)*(aVel-bVel)
- pendulumFrictionMassCoeff*bVel; // friction approximation
bVel += bAcc * dt;
b += bVel * dt;
// update pendulum tip path array
for (int i = 1; i < PATH_L; i++) {
// move all vertices of path one back in path array
path[i - 1] = path[i];
}
// add newest position at the end
path[PATH_L - 1] = V2(leg2pos.x + pendulumLength*sinf(b),
leg2pos.y + pendulumLength*cosf(b));
}
// -- drawing --
// draw pendulum tip path
v2sToPts(path, path_pts, PATH_L);
SDL_SetRenderDrawColor(gRenderer, 0, 0, 255, 255); // blue
SDL_RenderDrawLines(gRenderer, path_pts, PATH_L);
// draw support
SDL_SetRenderDrawColor(gRenderer, 0, 0, 0, 255); // black
drawRect(gRenderer, support.pos, V2(supportSize, supportSize), V2(0, 0), 0);
// draw support track
SDL_SetRenderDrawColor(gRenderer, 255, 0, 0, 255); // green
SDL_RenderDrawLine(gRenderer, supportTrackStart, supportTrackHeight, supportTrackEnd, supportTrackHeight);
// draw pendulum leg 1
SDL_SetRenderDrawColor(gRenderer, 255, 0, 0, 255); // red
drawRect(gRenderer, leg1pos, V2(pendulumWidth, pendulumLength), pendulumOrigin, a);
// draw pendulum leg 2
SDL_SetRenderDrawColor(gRenderer, 0, 0, 255, 255); // blue
drawRect(gRenderer, leg2pos, V2(pendulumWidth, pendulumLength), pendulumOrigin, b);
// render to screen
SDL_RenderPresent(gRenderer);
}
// sdl close
closeSDL();
return 0;
}